Naive Bayes Classifier

Understanding Bayes' Theorem

Naive Bayes is a classification algorithm that applies Bayes’ Theorem to estimate the probability of different outcomes based on given features.

Bayes’ Theorem describes conditional probabilities — for example, given that it’s cloudy outside, what’s the chance it’s going to rain?

That’s not the same as just asking, “What’s the chance of rain?” because now we’re factoring in something we know (that it’s cloudy) to update our guess. It shows how the probability of one event can change based on the occurrence of another event.

• P(Rain|Cloudy) = ?

This probability can be calculated using Bayes’ Theorem, which leverages what we know about other probabilities — like how often it rains in general (P(Rain)), how often it’s cloudy when it rains (P(Cloudy | Rain)), and how often it’s cloudy overall (P(Cloudy)).

By combining these, Bayes’ Theorem gives us an updated, more accurate guess about the chance of rain given that it’s cloudy.

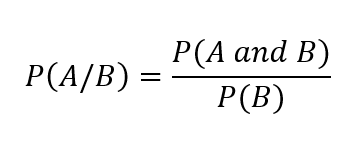
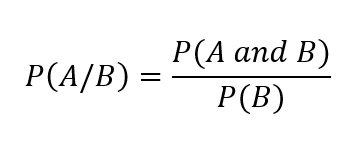
But here’s what that really means:

• P(A) is your prior probability — like your general belief about how often it rains.

• P(B|A) is the likelihood of seeing your evidence (cloudy skies) given its raining.

• P(B) is how common that evidence is overall — how often it’s just cloudy in general.

• P(A|B) is your updated belief: the chance it’s going to rain now that you know it’s cloudy.

So Bayes’ Theorem is really about understanding how the probability of one thing changes when you know something else is true.

It’s the foundation behind algorithms like Naive Bayes, where we use evidence from different features (like email words or weather conditions) to figure out the most likely outcome.

Bayes Theorem:

Naive Bayes Classifier

Let’s say you’re building a model to classify emails as spam or not spam. You have a dataset of emails that are already labeled (0 for not-spam, 1 for spam)— so for each one, you know whether it was spam and which words appeared in it.

For a new, unlabeled email, Naive Bayes wants to answer the question: “What’s the probability that this email is spam, given the words in it?”

In Bayes’ Theorem terms, we’re calculating the probability the email is spam given the words in the email (free, money, winner):

P(Spam|Words) = P(Spam)* P(free|Spam) * P(money|Spam) * P(winner|Spam)

• P(Spam): How likely any given email is to be spam, based on your dataset. If 20% of your emails are spam, then P(Spam) = 0.2.

• P(Words | Spam): How likely it is for those words to appear in a spam email. For example, if the word “free” appears in 70% of spam emails, then “free” is a strong signal for spam.

• P(Words): How often those words appear in any email — spam or not. This normalizes the score but can often be skipped in practice since it’s the same for every class and doesn’t affect the final choice.

• P(Spam | Words): This is the final probability we care about: how likely the email is spam given the words it contains.

After calculating the conditional probability for each word given a class (like spam), you multiply those probabilities together — along with the prior probability of the class — to get the overall likelihood that the message belongs to that class. This combined probability reflects how strongly the words, taken together, support the classification.

In this example, you would also calculate the probability for the other class — Not Spam — and then choose the class with the higher probability as the final prediction -> P(Spam | Words) or P(Not Spam | Words).

*There is no need to divide by P(Words) (like in the original Bayes' formula) because the denominator is the same for all class calculations, so it doesn’t affect which class has the highest probability.

Spam Email Example